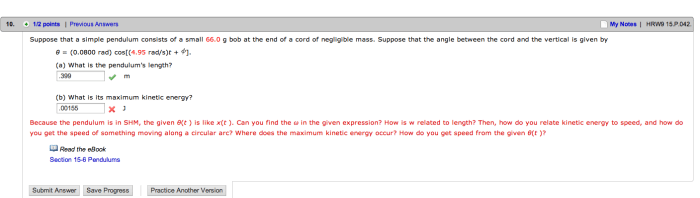
Suppose that a simple pendulum consists of a small, spherical mass suspended by a light, inextensible string. This seemingly simple system provides a fascinating platform to explore the fundamental principles of physics, from the interplay of forces to the measurement of time.
The study of simple pendulums has a rich history, dating back to the pioneering work of Galileo Galilei in the 16th century. Over the centuries, scientists have employed this elegant apparatus to unravel the mysteries of motion, gravity, and the nature of time itself.
Introduction: Suppose That A Simple Pendulum Consists Of A Small

A simple pendulum is a weight suspended from a fixed point by a string or wire. When the weight is displaced from its equilibrium position and released, it swings back and forth. The period of a pendulum is the time it takes for the weight to complete one full swing.
The period of a pendulum is affected by the length of the pendulum, the mass of the weight, and the amplitude of the swing.
Period of a Simple Pendulum, Suppose that a simple pendulum consists of a small
The period of a simple pendulum is given by the formula:
T = 2π√(L/g)
where:
- T is the period of the pendulum in seconds
- L is the length of the pendulum in meters
- g is the acceleration due to gravity in m/s^2
The period of a pendulum is directly proportional to the square root of the length of the pendulum. This means that a longer pendulum will have a longer period than a shorter pendulum.
Amplitude of a Simple Pendulum
The amplitude of a pendulum is the maximum angle that the pendulum swings from its equilibrium position. The amplitude of a pendulum affects its period. A pendulum with a larger amplitude will have a longer period than a pendulum with a smaller amplitude.
The amplitude of a pendulum can be changed by changing the initial displacement of the weight. A weight that is displaced further from its equilibrium position will have a larger amplitude than a weight that is displaced closer to its equilibrium position.
Applications of Simple Pendulums
Simple pendulums have a variety of practical applications. They are used in clocks, metronomes, and other timekeeping devices. They are also used in scientific instruments to measure acceleration and gravity.
In clocks, the period of a pendulum is used to regulate the speed of the clock. A longer pendulum will make the clock run slower, while a shorter pendulum will make the clock run faster.
Design a Simple Pendulum
To design and build a simple pendulum, you will need the following materials:
- A weight
- A string or wire
- A fixed point to hang the pendulum from
To assemble the pendulum, simply tie the weight to the end of the string or wire and hang it from the fixed point. The length of the pendulum can be adjusted by changing the length of the string or wire.
To measure the period of the pendulum, simply start the pendulum swinging and count the number of swings it makes in one minute. The period of the pendulum is equal to the number of swings divided by 60.
General Inquiries
What is the period of a simple pendulum?
The period of a simple pendulum is the time it takes for the pendulum to complete one full cycle, from one extreme position to the other and back again.
How does the length of the pendulum affect its period?
The period of a simple pendulum is directly proportional to the square root of its length. This means that as the length of the pendulum increases, its period also increases.
What are some applications of simple pendulums?
Simple pendulums have a wide range of applications, including clocks, metronomes, and seismometers. They are also used in scientific research to study the properties of materials and to measure the acceleration due to gravity.